The other night I found myself included on a message thread where a guy (this one) is attempting to develop a soccer Pythagorean formula that would allow him to predict the number of points won over a league season based on the number of goals scored and allowed by a team over a season.  From reading the website linked in the previous sentence, I suppose this Pythagorean is to be used to predict the odds of making the post-season playoffs or of winning the league championship or getting relegated in leagues that have either option.

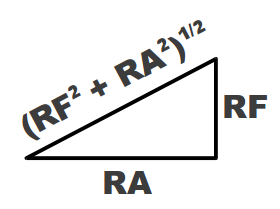
I’m embarrassed to admit that I didn’t know much about a Pythagorean before I got linked to this message, so I did a search and found this summary of a Pythagorean on Wikipedia.  It originated from Bill James and is derived as the following:

It appears that the key element of the Pythagorean is the exponent which is constant for all three terms in the expression.  A number of baseball sabermetricians have found that an exponent slightly less than 2 (1.81) provides a more accurate predictor of games won.  In basketball it’s a much larger value.  I have no idea what it is in soccer, or whether the exponent changes for different leagues and competitions.

There is a paper written by Steven Miller, a mathematics professor at Williams College, that gives a more theoretical underpinning to the Pythagorean.  I’ll take a look at the paper to see if I can glean anything interesting.  One item that jumps at me is that he assumes a Weibull distribution for runs scored in baseball.  Soccer goal distributions have been found to follow either a Poisson distribution or a negative binomial distribution.  Maybe it makes a difference, maybe it doesn’t, but we should find out either way.

I would like to see some statistical justification for the exponents that I’ve been seeing in some of the soccer Pythagorean formulae.

UPDATE (5 Feb 2013): Finally got around to correcting the Pythagorean distribution.