Assessing the Projections: 2015 Major League Soccer regular season
Categories: League Competitions, Soccer Pythagorean: Tables, Team Performance
The 2015 Major League Soccer regular season concluded last Sunday. It’s time to engage in that exercise in humility in which I look back at projections made at the start of the season and assess them.
Here is what was projected at the beginning of the season – first by conference:
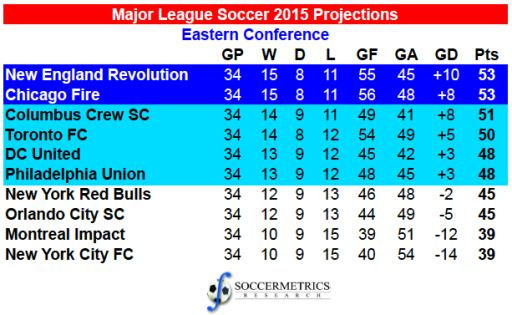
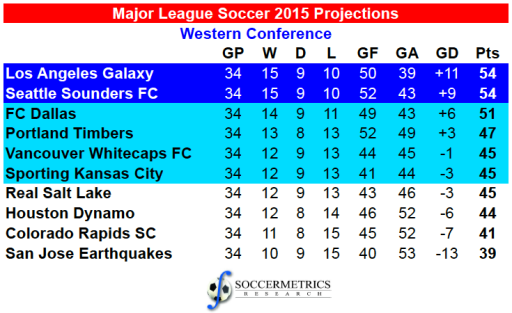
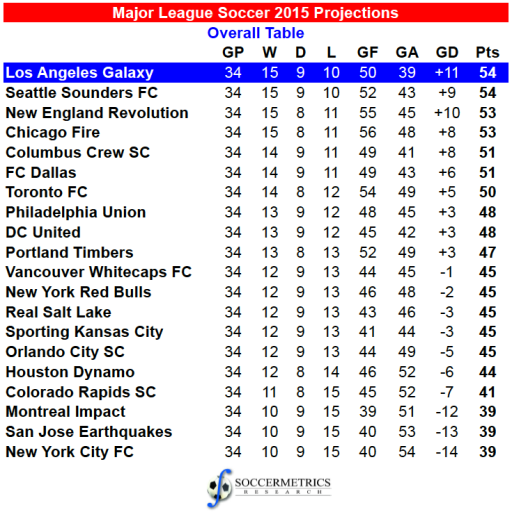
And then the single table:
The final league table finished like this at conference level, with Pythagorean expectations of the team records thrown in:
Eastern Conference:
| Standard Table | Pythagorean | ||||||||||||
| GP | W | D | L | GF | GA | GD | Pts | W | D | L | Pts | Δ | |
| New York Red Bulls | 34 | 18 | 6 | 10 | 62 | 43 | 19 | 60 | 17 | 8 | 9 | 59 | +1 |
| Columbus Crew SC | 34 | 15 | 8 | 11 | 58 | 53 | 5 | 53 | 14 | 8 | 12 | 50 | +3 |
| Montreal Impact | 34 | 15 | 6 | 13 | 48 | 44 | 4 | 51 | 13 | 9 | 12 | 48 | +3 |
| DC United | 34 | 15 | 6 | 13 | 43 | 45 | -2 | 51 | 12 | 9 | 13 | 45 | +6 |
| New England Revolution | 34 | 14 | 8 | 12 | 48 | 47 | 1 | 50 | 13 | 9 | 12 | 48 | +2 |
| Toronto FC | 34 | 15 | 4 | 15 | 58 | 58 | 0 | 49 | 13 | 8 | 13 | 47 | +2 |
| Orlando City SC | 34 | 12 | 8 | 14 | 46 | 56 | -10 | 44 | 11 | 8 | 15 | 41 | +3 |
| New York City FC | 34 | 10 | 7 | 17 | 49 | 58 | -9 | 37 | 11 | 8 | 15 | 41 | -4 |
| Philadelphia Union | 34 | 10 | 7 | 17 | 42 | 55 | -13 | 37 | 10 | 8 | 16 | 38 | -1 |
| Chicago Fire | 34 | 8 | 6 | 20 | 43 | 58 | -15 | 30 | 10 | 8 | 16 | 38 | -8 |
Western Conference:
| Standard Table | Pythagorean | ||||||||||||
| GP | W | D | L | GF | GA | GD | Pts | W | D | L | Pts | Δ | |
| FC Dallas | 34 | 18 | 6 | 10 | 52 | 39 | 13 | 60 | 15 | 9 | 10 | 54 | +6 |
| Vancouver Whitecaps FC | 34 | 16 | 5 | 13 | 45 | 36 | 9 | 53 | 14 | 10 | 10 | 52 | +1 |
| Portland Timbers | 34 | 15 | 8 | 11 | 41 | 39 | 2 | 53 | 13 | 10 | 11 | 49 | +4 |
| Seattle Sounders FC | 34 | 15 | 6 | 13 | 44 | 36 | 8 | 51 | 14 | 10 | 10 | 52 | -1 |
| LA Galaxy | 34 | 14 | 9 | 11 | 56 | 46 | 10 | 51 | 15 | 8 | 11 | 53 | -2 |
| Sporting Kansas City | 34 | 14 | 9 | 11 | 48 | 45 | 3 | 51 | 13 | 9 | 12 | 48 | +3 |
| San Jose Earthquakes | 34 | 13 | 8 | 13 | 41 | 39 | 2 | 47 | 13 | 10 | 11 | 49 | -2 |
| Houston Dynamo | 34 | 11 | 9 | 14 | 42 | 49 | -7 | 42 | 11 | 9 | 14 | 42 | 0 |
| Real Salt Lake | 34 | 11 | 8 | 15 | 38 | 48 | -10 | 41 | 10 | 9 | 15 | 39 | +2 |
| Colorado Rapids SC | 34 | 9 | 10 | 15 | 33 | 43 | -10 | 37 | 10 | 10 | 14 | 40 | -3 |
The final single table looks like this:
| Standard Table | Pythagorean | ||||||||||||
| GP | W | D | L | GF | GA | GD | Pts | W | D | L | Pts | Δ | |
| New York Red Bulls | 34 | 18 | 6 | 10 | 62 | 43 | 19 | 60 | 17 | 8 | 9 | 59 | +1 |
| FC Dallas | 34 | 18 | 6 | 10 | 52 | 39 | 13 | 60 | 15 | 9 | 10 | 54 | +6 |
| Vancouver Whitecaps FC | 34 | 16 | 5 | 13 | 45 | 36 | 9 | 53 | 14 | 10 | 10 | 52 | +1 |
| Columbus Crew SC | 34 | 15 | 8 | 11 | 58 | 53 | 5 | 53 | 14 | 8 | 12 | 50 | +3 |
| Portland Timbers | 34 | 15 | 8 | 11 | 41 | 39 | 2 | 53 | 13 | 10 | 11 | 49 | +4 |
| Seattle Sounders FC | 34 | 15 | 6 | 13 | 44 | 36 | 8 | 51 | 14 | 10 | 10 | 52 | -1 |
| Montreal Impact | 34 | 15 | 6 | 13 | 48 | 44 | 4 | 51 | 13 | 9 | 12 | 48 | +3 |
| DC United | 34 | 15 | 6 | 13 | 43 | 45 | -2 | 51 | 12 | 9 | 13 | 45 | +6 |
| LA Galaxy | 34 | 14 | 9 | 11 | 56 | 46 | 10 | 51 | 15 | 8 | 11 | 53 | -2 |
| Sporting Kansas City | 34 | 14 | 9 | 11 | 48 | 45 | 3 | 51 | 13 | 9 | 12 | 48 | +3 |
| New England Revolution | 34 | 14 | 8 | 12 | 48 | 47 | 1 | 50 | 13 | 9 | 12 | 48 | +2 |
| Toronto FC | 34 | 15 | 4 | 15 | 58 | 58 | 0 | 49 | 13 | 8 | 13 | 47 | +2 |
| San Jose Earthquakes | 34 | 13 | 8 | 13 | 41 | 39 | 2 | 47 | 13 | 10 | 11 | 49 | -2 |
| Orlando City SC | 34 | 12 | 8 | 14 | 46 | 56 | -10 | 44 | 11 | 8 | 15 | 41 | +3 |
| Houston Dynamo | 34 | 11 | 9 | 14 | 42 | 49 | -7 | 42 | 11 | 9 | 14 | 42 | 0 |
| Real Salt Lake | 34 | 11 | 8 | 15 | 38 | 48 | -10 | 41 | 10 | 9 | 15 | 39 | +2 |
| New York City FC | 34 | 10 | 7 | 17 | 49 | 58 | -9 | 37 | 11 | 8 | 15 | 41 | -4 |
| Philadelphia Union | 34 | 10 | 7 | 17 | 42 | 55 | -13 | 37 | 10 | 8 | 16 | 38 | -1 |
| Colorado Rapids SC | 34 | 9 | 10 | 15 | 33 | 43 | -10 | 37 | 10 | 10 | 14 | 40 | -3 |
| Chicago Fire | 34 | 8 | 6 | 20 | 43 | 58 | -15 | 30 | 10 | 8 | 16 | 38 | -8 |
When I ran the numbers on this season’s collection of projections, I was starting to feel bad, but then I compared them to last year’s performance and I felt slightly better but still depressed. Preseason projections are always going to be a bit unreliable when it comes to point totals, but I do believe that a model that’s good enough contains some nugget of reality about each team’s chances. That said, small differences manifested themselves into significant deviations from reality.
As was the case last season, the current projection model does a good job of predicting the teams that do make it to the MLS Cup Playoffs: four of the six teams in the Eastern Conference, and five of the six teams in the West. To be fair, it’s a little misleading to look at accuracy alone, so here is a confusion matrix of the projection model’s performance:
| Predicted | |||
| Playoffs | No Playoffs | ||
| Actual | Playoffs | 9 | 3 |
| No Playoffs | 3 | 5 | |
If we’re using the projection model to predict, or, in machine learning language, classify who will go to the playoffs (not the original intent, but just for sake of argument), the accuracy rate of this season’s model is 70% (14 correct predictions — 9 in playoffs, 5 out of playoffs — out of 20). Because the model always classifies 12 teams for the playoffs, the recall and precision rates are identical: 75% (9 of 12). Overall the model’s playoff prediction error is a little better than blindly predicting that all teams will make the playoffs (30% versus 40%), but not much more.
If we’re using the projection model to predict points and places, it does a less impressive job. The RMSE of the final position in the projection model is about 40% worse than last season’s model, but the RMSE of the final point total is about the same as last season’s (8.3126 vs 8.3161). The preseason model predicted a closely contested regular season, with just nine points separating first place from 13th, which meant that any deviation in points would result in a significant rise or fall in the league table. That result comes down to the quality of the expected goals that are fed into the Pythagorean expectation to predict total points.
There are always projections that are spot on, and some that are true clangers. The biggest misses in a positive direction were New York Red Bulls and Montreal Impact, who performed at least 12 points ahead of expectations. Both teams were characterized by offensive and defensive goal statistics that ran well ahead of expectations, but Montreal received a huge boost from the summer signing of Didier Drogba. The biggest misses in a negative direction were Philadelphia Union and Chicago Fire — both teams performed 11 and 23 points below expectations, respectively, and both sides had the worst combined offensive and defensive goal performance relative to preseason expectations. Little wonder that the Union made a big change at the front office; the Fire are expected to do the same. The few projections that were spot on were Columbus Crew SC, DC United, Orlando City SC, and Houston Dynamo. Finally it’s worth saying that of the teams performing at least five goals better in defense than expected, only the San Jose Earthquakes missed the playoffs. Sporting Kansas City, who earned the final Western playoff spot at the Quakes’ expense, allowed one more goal than expected preseason. (But again, did the teams really perform that well, or did it appear that way thanks to a biased expected goals model?
Let’s assume that we did have a model that projected the expected goals for each team perfectly. The Pythagorean expectation would look like the last five columns in the final tables listed above. In this context, the point totals represent expected points for an average team with identical goal statistics. The RMSEs of the final points and positions are greatly reduced (3.44 points and 2.43 places, respectively), and if you look at individual teams the deviation between prediction and reality is much smaller. Nevertheless, you can identify some teams that appear to have over- or under-performed their expectations. DC United and FC Dallas had Pythagorean residuals of +6, which would have made a difference in United’s position in the table but not much in their playoff destiny (perhaps, they would have had an away knockout match in the playoff). At the other end of the scale, Chicago’s -8 Pythagorean residual meant that when it rained, it poured.
If we make another confusion matrix for the Pythagorean expectation (perfect expected goals model), we get the following result:
| Predicted | |||
| Playoffs | No Playoffs | ||
| Actual | Playoffs | 11 | 1 |
| No Playoffs | 1 | 7 | |
This gives an accuracy rate of 90% (18/20) and recall/precision of 91.6% (11/12). Which of course is fantastic, but it’s easier to give more accurate predictions with perfect data.
Statistical Summary:
| Pred Goals | Actual Goals | % Diff Goals | RMSE Pts | RMSE GF | RMSE GA | RMSE Pos |
| 938 | 937 | -0.10% | 8.31 | 7.88 | 7.63 | 6.89 |
This season’s projection will hopefully be the last of these league projections as currently designed. I’m a relative newcomer to predictive analytics in football, and I’ve viewed these attempts at league projection as a learning experience and a bit of a challenge. I’ve definitely learned a lot, chief among them the need to have ownership over the expected (or projected) goal models and a more systematic and quantitative assessment of the uncertainty present in these expectations/projections. I don’t know when the new version of the league projection will be ready, but the plan is to develop expected goal models that a bit less opaque and deploy uncertainty bounds around the point projections. In other words, go Bayesian.

