En los últimos años, la expectativa de gol (xG en inglés) ha llegado a ser la medida del análisis avanzado con el mayor impacto en el mundo del fútbol.  Dentro de la comunidad del análisis estadístico de fútbol, parece que todo el mundo ha desarrollado su modelo estadístico de expectativa de gol para hacer una narrativa de las tendencias de cuadros, jugadores, y estrategias.  En cuanto al Soccermetrics, en 2009 la primera entrada de esta bitácora discutió el concepto de esta expectativa:

Creo que estas medidas útiles van a contribuir hacia un “valor expectativa de gol” — la probabilidad de crear un gol por tal juego en la cancha durante el partido. Los juegos que pertenecen a las distintas posiciones requieren ciertos datos específicos…

–“Moneyball and soccer“, 8 de enero de 2009 (traducción mía)

En 2011 inicié algunos cálculos de la probabilidad de gol por escenarios distintos que ya se encuentran el los modelos xG, pero no terminé el proyecto por motivo de prioridades otras.  Durante los años intermedios surgieron los analistas que presentaron sus modelos xG al mundo — gente como Michael Caley y Sander Ijtsma (11tegen11), y proyectos colectivos como American Soccer Analysis y StatsBomb.  Además hay analistas quien ha discutido los xG en el idioma español; Informe de Fútbol es un ejemplo.

Luego de tantos años, y luego de tantas presentaciones de los demás analistas, es hora preguntar, “¿Cómo no yo?” Es hora poner en práctica lo aprendido del aprendizaje automático y del modelaje de datos.  Es hora poner en abierto mis esquemas de crear modelos xG – la elección de los atributos del modelo, la preparación de los datos, la estrategia de entrenar y evaluar a los modelos, y más.  No recorro tierra desconocida en esta entrada, pero si lo que escribo te ayuda, mejor.  En el futuro cercano, comparto en el GitHub el código informático que desarrollé para hacer los modelos xG.

Los datos, la pregunta eterna

Todos los modelos estadísticos requieren un histórico de datos para desarrollar una hipótesis sobre el mundo.  Este histórico debe contener instancias diversas y atributos diversos para poder identificar los patrones que caracterizan los tiros que lanzan en un partido.  Suele requerir una cantidad masiva de datos para aprender los patrones con alto grado de acierto — decenas y hasta cientos de miles de tiros durante varios años.  Adquirir este histórico requiere comprar datos de los proveedores de datos deportivos, que resulta ser una tarea muy cara.

Para este proyecto uso datos de las distintas empresas (Opta, DataFactory, Stratagem), pero para entrenar a los modelos xG uso el muy impresionante almacén de datos de Christopher Long, que es estadístico y un analista famoso de algunos equipos de deporte.  El histórico de Long es masivo, pero no es perfecto, así que uno debe contestar la pregunta, “¿Qué es lo fundamental de la expectativa de gol?“

Qué es la expectativa de gol?

El modelo de la expectativa de gol es un modelo de la probabilidad condicional.  Contesta la pregunta, “¿Qué es la probabilidad de marcar un gol de un tiro, dado que el tiro se lleva tal colección de atributos?“

Digamos que \(\mathbf{x}\) representa los atributos del tiro, y \(G\) el evento de gol. En el idioma de la matemática, se escribe la probabilidad condicional así:

\[
Pr(G|\mathbf{x}) = f(\mathbf{\beta}, \mathbf{x})
\]

en que \(\mathbf{\beta}\) representa los coeficientes que corresponden a los atributos de tiro, y la ‘|’ representa el “dado que” de aquél pregunta.

Los tiros son eventos binarios (gol o no gol) que llevan una probabilidad de gol entre 0 y 1, así que hay una función que representa esta relación muy bien.  Esa función se llama una sigmoide:

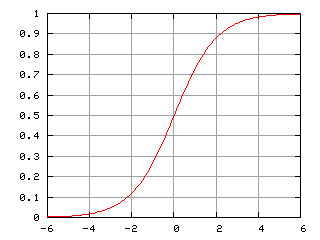
Curva de la función logística (una sigmoide). Desde CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=644559

La colocamos en el lado derecho de la probabilidad condicional:

\[
Pr(G|\mathbf{x}) = \frac{1}{1 + e^{-\mathbf{\beta}^T\mathbf{x}}}
\]

Cuáles atributos de tiro importan?

La selección de los atributos de tiro para el modelo xG diferencia un modelo al otro, y es producto del conocimiento, el juicio, y la experiencia del analista.  Prefiero eligir atributos comunes a los históricos de datos que hay para entender cuáles son los más importantes.

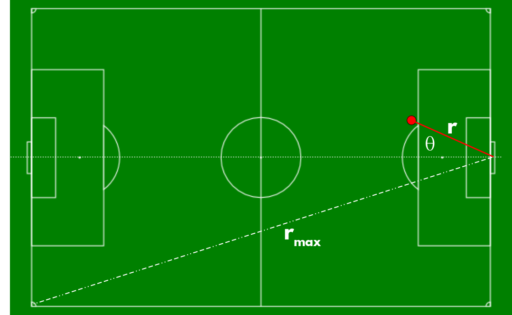
Diagrama de un tiro al arco en el fútbol.  Se mide la distancia del punto (x,y) del tiro (el punto rojo) al centro de la línea del gol.

Distancia: Claro que un tiro más cercano al arco lleva mayor posibilidad de convertirse en gol.  Se mide la distancia del punto \((x,y)\) del tiro al centro de la línea del gol y se divide por la máxima distancia \(r_{max}\) del centro de la línea del gol al córner más lejano para que la distancia esté entre 0 y 1.

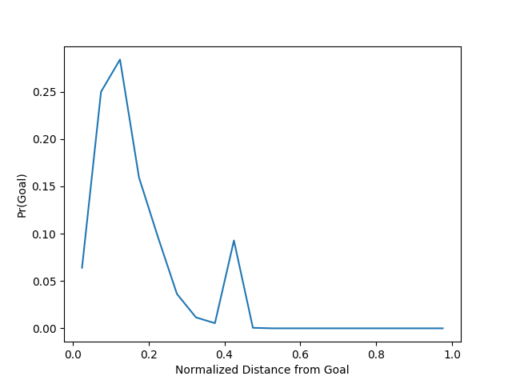
La probabilidad de gol como una función de la distancia normalizada. Datos son del partidos de la Primera División Argentina, años 2007-2014. Fuente: Christopher Long

Ángulo: Además, claro que un tiro ejecutado desde el centro el campo lleva mayor probabilidad de convertirse que uno al ángulo extremo.  Se define como el ángulo entre el vector de distancia y la línea central entre los dos líneas del gol, y los tiros ejecutados desde el lado izquierdo tienen un ángulo positivo.  Se divide el ángulo por \(\frac{\pi}{2}\) para que el resultado esté entre 0 y 1.

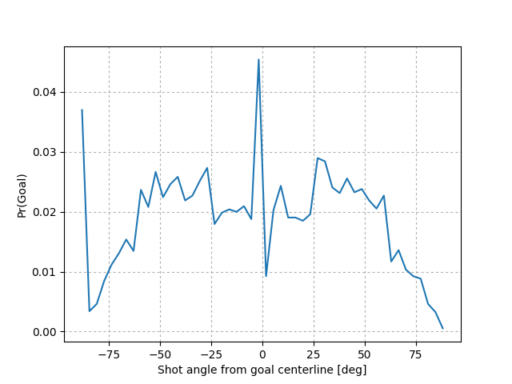
La probabilidad de gol como una función del ángulo del tiro. Datos son del partidos de la Primera División Argentina, años 2007-2014. Fuente: Christopher Long

Marcador: Si bien este atributo no refleja ningún característico físico, algunos analistas (entre ellos el 11tegen11) han notado su importancia en el modelo xG.  También se llama “estado del partido” (match state en inglés) y se define como la diferencia de gol \(\Delta\) con respeto al equipo del tirador — si equipo A le gana al equipo B por 2-0 y un jugador del B hace un tiro, el estado del partido es -2.  Se usa la función logística para modificar la escala a un número entre 0 y 1:

\[
\Delta’ = \frac{2}{1 – e^{-\Delta}} – 1
\]

Tiempo del juego: Otro atributo que no refleja ningún característico físico del tiro pero sí lleva efecto en la probabilidad de gol.  El tiempo del tiro se divide por la duración el período en que ocurre (45 minutos más descuento) para que 0.5 (0,5) representa el medio tiempo y 1.0 (1,0) el final del partido.  Sólo considera los partidos de 90 minutos, pero anticipo que en los partidos con alargue el tiempo de juego va al 2.0.

Tipo de juego: Hay una multitud de tipos de juego que resultan en un tiro al arco.  En este modelo diferencian entre los que ocurren en juego abierto, los que ocurren por juegos de balón parado, y los tiros de penalti.  Otros analistas lo diferencian aún más si el histórico de datos es suficientemente detallista.

Parte de cuerpo: Este atributo es obvio (no hablemos de manos de Dios).  Usan ciertos partes del cuerpo más seguido para hacer tiros al arco luego de ciertas jugadas (la cabeza luego de un centro, o los pies luego de un pase por el medio).  Algunas empresas incluyen este dato, otras lo hacen en una manera incompleta (ej. notar goles de cabeza pero no todos los tiros de cabeza).  Usar este atributo depende en la calidad del histórico de datos.

Torneo o País: Hay algunos que usan este atributo para notar la diferencia de desempeño entre los diversos torneos. Para mí, parece mejor entrenar a los modelos que corresponden a cada competición (o sea, competiciones relacionadas) en vez de mezclar datos, o quizás entrene a un modelo con datos de campeonatos parecidos (ej. todo de primera nivel).

Cómo entrenar al modelo?

Para entrenar al modelo xG, prefiero usar herramientas disponibles de computación ya probadas y optimizadas.  Por eso, uso el programa scikit-learn (algoritmo LogisticRegression).

La mayoría del laburo se encuentra en la colección del histórico de datos, organizado al nivel de partidos.   Mejor dividir el histórico en dos partes:

• Un 25% del histórico se dedica a pruebas del modelo entrenado. El modelo nunca ve este segmento durante el proceso del entrenamiento.  Para el xG aguardo los datos de uno o dos torneos completos para evaluar el desempeño del modelo.
• El resto del histórico para entrenar y evaluar al modelo, implementando una validación cruzada de k iteraciones para evaluar los parámetros del algoritmo.  Reparte el histórico al nivel de partidos, para que todos los tiros de un partido pertenecen al conjunto de muestra o el de prueba.

Muchos analistas prefieren usar la coeficiente del determinación \(R^2\) para evaluar la calidad del modelo entrenado.  Para mí es una medida media engañosa que aumenta al agregar más variables en el modelo, y además prefiero analizar la calidad de predicción.  Por eso uso la calificación Brier para comparar la expectativa de probabilidad de gol al resultado real.

Demostración #1: Primera División Argentina

Bueno, demostremos el modelo xG al campeonato de la Primera División Argentina. Lo evalúo durante dos temporadas: el Torneo Largo del 2015, y el Torneo Transición de 2016.  Algunos analistas destacan la capacidad predictiva de la expectativa de gol, así que vamos a realizar algunas pruebas a ver si observe lo mismo.

Arreglo un modelo xG con atributos de distancia, ángulo, estado del partido, tiempo de juego, y tipo de juego (jugadas de penal o no). El histórico de datos para entrenar al modelo son de la Primera División Argentina entre los años 2007 y 2014, pero no diferencian entre el juego abierto y el balón parado.

Las primeras ilustraciones demuestran la relación estadística entre la expectativa de gol y la cantidad real, tanto marcado como recibido.  Calculo el coeficiente de correlación para los dos pares de datos.  En el Torneo Anual de 2015, la expectativa de gol tiene un relación fuerte y positiva con la cantidad de gol, pero en el Torneo de Transición esta relación se ve reducida. ¿Puede ser el cambio del formato de un año al otro?

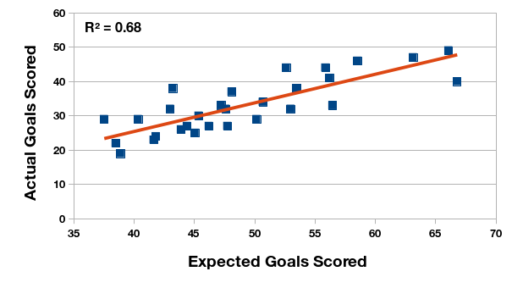
Relación entre la expectativa de gol marcados y los goles marcados en realidad, Campeonato de Primera División 2015 (Argentina).

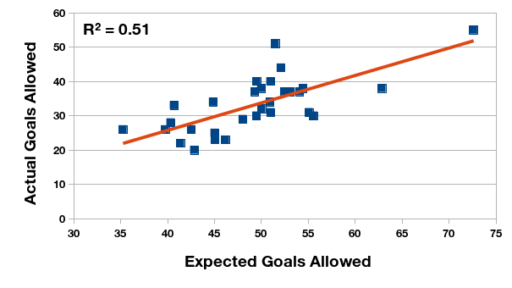
Relación entre la expectativa de gol recibido y los goles recibidos en realidad, Campeonato de Primera División 2015 (Argentina).

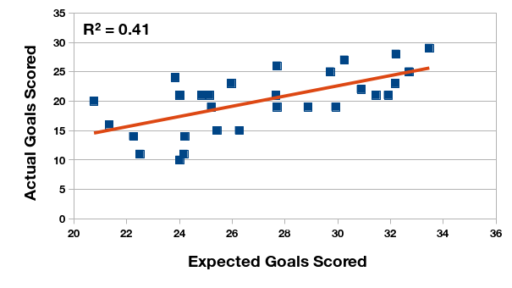
Relación entre la expectativa de gol marcados y los goles marcados en realidad, Campeonato de Primera División 2016 (Argentina).

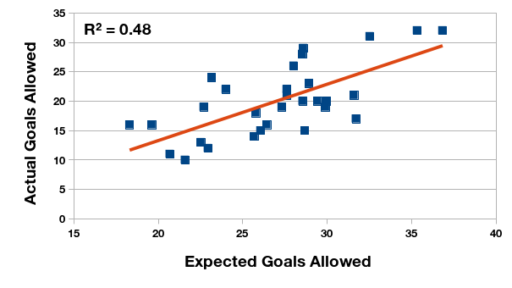
Relación entre la expectativa de gol recibido y los goles recibidos en realidad, Campeonato de Primera División 2016 (Argentina).

Una característica de la expectativa de gol es la estabilidad de su medida durante temporadas múltiples. Si se define la tasa xG

\[
xG\% = \frac{\hat{G}_M}{\hat{G}_M + \hat{G}_R}
\]

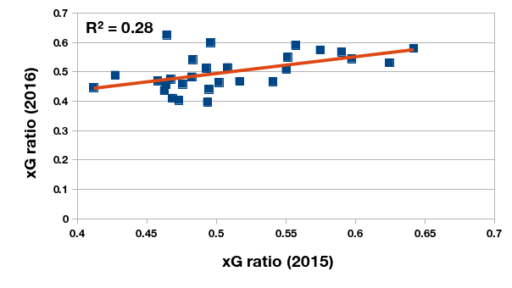
en que \(\hat{G}_M\) es la expectativa de gol marcado y \(\hat{G}_R\) la expectativa de gol recibida, ¿es una medida más creíble para estimar la potencia de largo plazo de un equipo?  Evalúo esta pregunta por comparar la tasa xG del los 28 equipos de Primera que permaneció en la división durante el 2015 y 2016.  La relación entre la tasa xG de los dos temporadas consecutivas no es tan fuerte como lo observado por demás analistas, pero es muchísimo más fuerte que la relación del promedio de puntos durante las mismas temporadas. Puede ser que la volatilidad del plantel y el cuerpo técnico contribuyan a la baja nivel de correlación.

La tasa xG de los 28 clubes de Primera que permanecieron en la división entre 2015 y 2016.

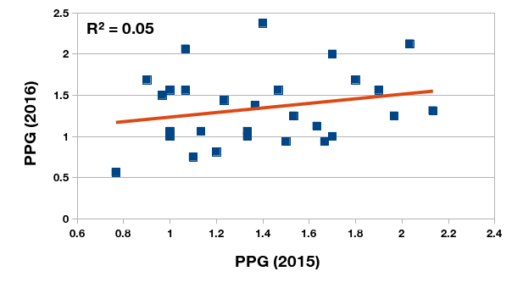
Los promedios (de una sóla temporada) de los 28 clubes de Primera que permanecieron en la división entre 2015 y 2016.

Finalmente, compara la capacidad predictiva de la tasa xG con las tasas comunes en el análisis estadístico de fútbol — promedio de puntos, tasa de gol, tasa de tiros al arco (TSR por sus siglas en inglés).  Este estudio es una réplica de lo que hizo 11tegen11 cuando presentó su modelo xG.  Para cada fecha del torneo (menos la última), calcula el coeficiente de correlación entre la tasa válida para todos los partidos jugados hasta la fecha y la tasa válida para todos los partidos jugados después.  Las ilustraciones siguientes demuestran la tendencia de correlación como función de la fecha del torneo.  A lo largo del campeonato de 2015 la capacidad predictiva de la xG es más fuerte que la de TSR pero menos que el promedio de puntos y la tasa de gol.  Pero en las últimas cuatro o cinco fechas del campeonato, la expectativa de gol y la tasa de tiros al arco llevan más capacidad predictiva.  Los resultados del campeonato 2016 son los más interesantes — la capacidad predictiva de la xG está claramente menor que las demás medidas durante todo el torneo.  No sé por qué ocurre pero se merece una revisión más detallada.

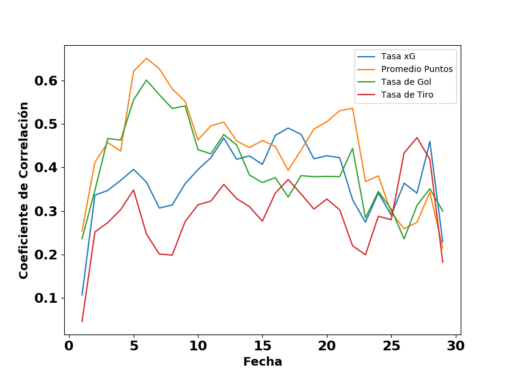
La comparación de la capacidad predictiva de algunas medidas avanzadas en el Campeonato de Primera División 2015 (Argentina).

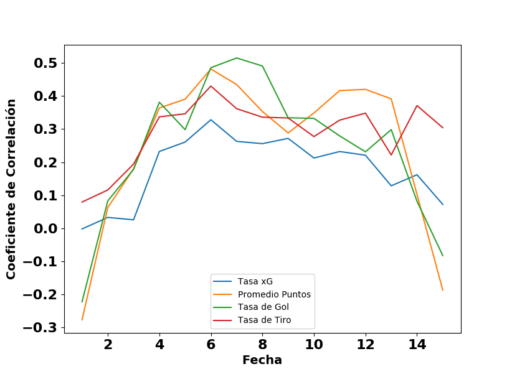
Comparación de la capacidad predictiva de algunas medidas avanzadas en el Campeonato de Primera División 2016 (Argentina).

Demostración #2: Segunda Bundesliga de Alemania

Esta estrada ya está larguísima, pero quiero demostrar la capacidad de la expectativa de gol en otro torneo: la Segunda Bundesliga de Alemania de la temporada 2010/11.  Se juega como la mayoría de las ligas europeas — un torneo a doble vuelta, con ascenso y descenso al final del campeonato.  Repetimos las pruebas que hicimos en la sección anterior, pero con un modelo distinto.

Este modelo xG tiene atributos de distancia, ángulo, estado del partido, tiempo de juego, tipo de juego (abierto, balón parado, penal), y parte de cuerpo. El histórico de datos para entrenar al modelo es de las mayores cinco ligas europeas (Premier League de Inglaterra, Primera de España, Ligue 1 de Francia, Serie A de Italia, Primera Bundesliga de Alemania) entre 2010 y 2011, y el archivo es bastante detallista para sacar más atributos de los tiros.

La siguiente ilustración demuestra la relación estadística entre la expectativa de gol y la cantidad real, tanto marcado como recibido.  Hay una fuerte relación positiva entre la expectativa de gol y la cantidad real de goles, a niveles parecidas de que observan otros analistas.

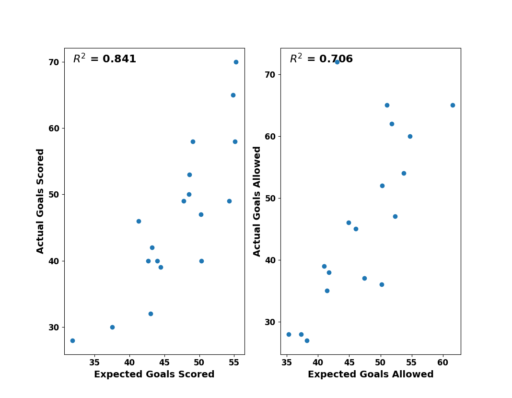
Relación de la expectativa de gol con la cantidad de gol de cada equipo, Campeonato de 2. Bundesliga de Alemania 2010/11.

La segunda ilustración compara la capacidad predictiva de la tasa xG con las tasas comunes en el análisis estadístico de fútbol.  La expectativa de gol tiene una capacidad predictiva más fuerte que las demás medidas durante la primera mitad del torneo alemán, también una observación que notan muchos analistas.  Puede ser que el histórico de datos lleve más patrones por ser más detallista, que resulte en la mayor capacidad predictiva.

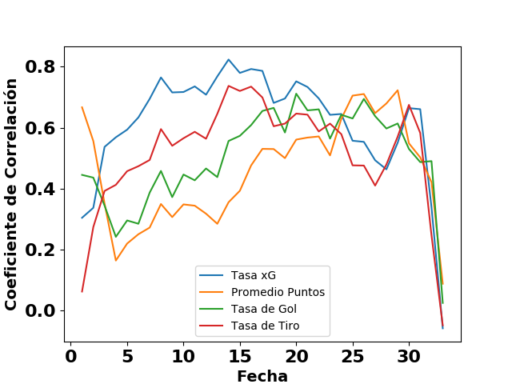
Comparación de la capacidad predictiva de algunas medidas avanzadas en el Campeonato de 2. Bundesliga de Alemania (2010/11).

Conclusiones

La expectativa de gol es una medida avanzada de fútbol que llegó para quedarse.  En los últimos años los analistas han aplicado este principio de expectación estadística a las demás jugadas en el fútbol, desde las asistencias y las atajadas hasta los pases y intervenciones defensivas.  Parece que la expectativa de gol captura algunas características del desempeño individual y colectivo, pero las características únicas de los torneos siguen siendo importantes.  Al final de todo, la expectativa de gol se merece su lugar en la caja de herramientas de los analistas avanzados de fútbol, y espero incorporarlo en adelante.